статьи про
самоподобные процессы
Асимметричная рефлексия, Золотая
Пропорция
и алгоритм «Вальс»
Калюжный О.Н.
2008
1.
Асимметричная рефлексия
В последние годы появилось много статей, авторы которых пытаются объяснить явление самоподобия, столь часто встречающееся в наблюдаемых случайных процессах. Как правило, в этих работах делаются попытки прийти к самоподобию процесса, отталкиваясь от классических вероятностных моделей, усложняя эти модели. Например, Б.С.Цыбаков доказал, что самоподобным является процесс, образованный из серий, «появление» которых подчиняется закону Пуассона. Такое объяснение, помимо математического изящества, хорошо обосновано «физически». Скажем, в случае наблюдения самоподобного интернет-трафика можно представить себе такую картину: новый пользователь включает компьютер, подключается к интернету и генерирует трафик. Тем самым он образует серию сигналов. Серия имеет свое начало, конец и является отрезком случайного процесса какого-то типа с какими-то характеристиками. Загруженность сервера, обслуживающего несколько таких пользователей, представляет собой самоподобный процесс и, с другой стороны, является суммой таких серий.
Однако самоподобие процессов, как известно, наблюдается и во многих других областях; одно из наиболее известных его проявлений – популярные некоторое время назад «Волны Эллиотта», то есть процесс колебания биржевых котировок, исследованный американским экономистом Эллиоттом. Одно из ключевых мест теории Эллиотта и его последователей – постоянное присутствие в кривых Золотой Пропорции, обеспечивающей подобие графиков котировок на крупных и мелких масштабах времени.
Теория
Эллиотта – чисто «описательная», она не содержит сколько-нибудь приличной
математической модели, но основывается на большом количестве наблюдений.
Главное ее достижение, на мой взгляд, следующее: экспериментально показано, что
Золотая Пропорция, т.е. ![]() , встречается в наблюдаемых самоподобных
процессах «очень часто».
, встречается в наблюдаемых самоподобных
процессах «очень часто».
В моей статье «О рекурсивности психического процесса принятия решения» (2005г.) рассмотрено асимметричное решающее правило, которое заключается в следующем. Перед субъектом стоит задача выбора между двумя решениями. Каждое из решений кажется ему одинаково хорошим (на сознательном уровне). Однако, на подсознательном уровне одно из решений имеет приоритет, хотя субъект об этом не догадывается. Вследствие этого (такова гипотеза) алгоритм принятия решения выглядит следующим образом.
Предположим, необходимо выбрать одно из двух решений: A0 («подсознательно правильное») и B0 («подсознательно неправильное»).
1.1 На первом шаге субъект с вероятностью ½ выбирает решение A0 и с вероятностью ½ - решение B0. В случае выбора A0 рассуждения прекращаются, решение является окончательным. В случае выбора B0 решение – не окончательное, субъект сомневается: «А правильное ли решение я принял?» Перед ним встает проблема выбора между двумя решениями следующего уровня: A1 («решение B0 - правильное») и B1 («решение B0 - неправильное»).
1.2 Если субъект принимает решение A1 (с вероятностью ½), это решение является окончательным и, следовательно, и решение B0 принимается окончательно. В случае выбора B1 рассуждения продолжаются на более «глубоком» уровне, т.е. речь идет о правильности выбора B1. И так далее: B2, B3, B4, …
2.1 На каждом из уровней, в случае неутверждения Bi+1 , рассуждения возвращаются к проблеме выбора между Ai и Bi .
Вероятно, словесное описание этого алгоритма является тяжелым для восприятия, но все становится понятным, если посмотреть на Рис.1.
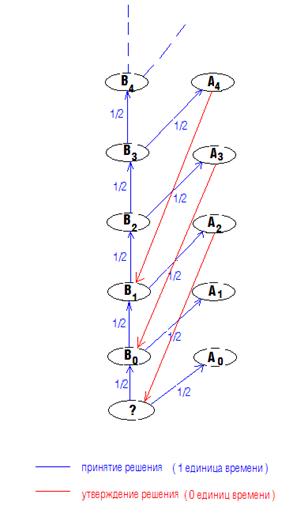
Рис.1
В упомянутой
выше статье показано, что данный
алгоритм приводит к принятию решения A0 с вероятностью 0,618… = ![]() = τ -1 и к принятию B0 с вероятностью
0,381… = τ -2 (τ будем называть Золотой Пропорцией,
τ -1 – Золотым Сечением;
τ -1 + τ -2 = 1 ).
= τ -1 и к принятию B0 с вероятностью
0,381… = τ -2 (τ будем называть Золотой Пропорцией,
τ -1 – Золотым Сечением;
τ -1 + τ -2 = 1 ).
2.
Блуждание по бесконечному графу
Легко заметить сходство между Рис.1 и Рис.2, иллюстрирующем мой алгоритм «Вальс» (см. статью).
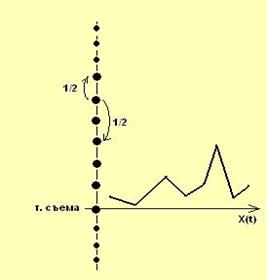
Рис.2
Разница между алгоритмом асимметричной рефлексии и (Рис.1) и алгоритмом «Вальс» (Рис.2) состоит в том, что во втором случае граф представляет собой последовательность вершин, бесконечную как вверх, так и вниз. Кроме того, по графу движется сразу n объектов, а не 1, как в первом случае. Общая для обоих алгоритмов идея – «Шаг вперед – два шага назад». То есть рассуждения либо, с вероятностью ½ , идут «вглубь», либо, с вероятностью ½ , очередное решение утверждается и мы откатываемся на два уровня назад.
Посмотрим, где скрывается Золотая Пропорция в алгоритме «Вальс». Найдем равновесное расположение количества объектов («шариков») по графу.
Пусть в i-й вершине в случае равновесного расположения находится в среднем qi = 1 шарик. Предположим, что при таком расположении количества на соседних уровнях различаются в q раз: qi = q –i (q≥1). Найдем константу q.
На любом шаге алгоритма все шарики перемещаются из вершины i в вершину (i+1) и в вершину (i-2). Взамен в i-ю вершину приходят шарики из вершин (i+2) и (i-1). В среднем в i-й вершине оказывается следующее количество объектов:
qi = ½ * qi-1
+ ½ * qi+2 ;
qi = 1, qi = q –i =>
=> 1 = ( q + q -2 ) * ½ = ( q 3 + 1 ) /
( 2 q 2 ) ;
q 3 – 2 q 2 + 1 = 0
; (*)
Это уравнение
имеет 2 положительных решения: τ = 1,618 … и 1.
Таким образом, в алгоритме «Вальс» также присутствует Золотая Пропорция.
3.
Стабилизация на экспонентах
Обратимся к этому алгоритму и обозначим X(t) число шариков в 0-й вершине («точке съема сигнала») в момент t. X(t) - самоподобный случайный процесс, зависящий от начального расположения шариков на графе. Начальное расположение может быть как равномерным, так и любым другим: например, на нескольких соседних вершинах наверху графа находится по N штук, в остальных вершинах – по 0 штук. С ходом времени такой «импульс» сползает вниз и «расплывается»; когда он доходит до точки съема, он представляет собой «горб», немного похожий на график нормальной плотности, но асимметричный и зубчатый.
Решения уравнения (*) говорят о том, что стабилизация процесса X(t) возможна, по крайней мере, в двух случаях:
1. Когда шарики в узлах, близких к точке съема, распределились равномерно;
2. Когда распределение шариков в узлах, близких к точке съема, убывает снизу вверх как τ -i.
На Рис.3 изображен случай прохождения локального импульса, «запущенного» из удаленной вершины. Как только остатки импульса выстраиваются как последовательность с определенными свойствами, процесс стабилизируется.
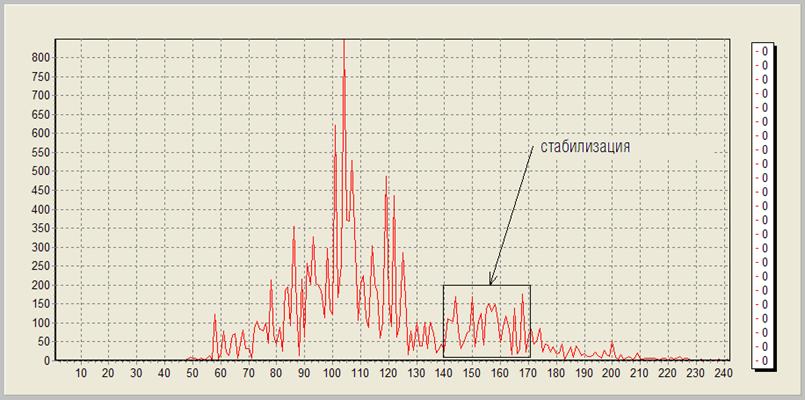
Рис.3
Смоделировать вырожденный случай стабилизации можно, расположив на графе числа Фибоначчи (как известно, предел отношения соседних чисел Фибоначчи равен τ). Сделать это можно с помощью программы Waltz, нажав кнопку «Ф» в разделе «Размещение на антенне». Конечно, построить бесконечную последовательность чисел физически невозможно, поэтому числа располагают в районе точки съема: в 2n узлах – выше и в n узлах – ниже точки. После запуска алгоритма процесс ведет себя стабильно до тех пор, пока не дает о себе знать обрыв последовательности сверху и снизу.
Парадоксальность этого явления состоит в том, что возрастание/убывание процесса зависит не только от возрастания/убывания входящего сигнала, но и от характера этого сигнала, то есть от того, на что в данный момент больше всего похож сигнал в районе точки съема: на экспоненту, прямую, логарифм или на что-то еще. То есть алгоритм способен преобразовывать достаточно гладкий входящий сигнал в самоподобный, хаотичный процесс.
Обратим внимание на суть нашего способа размещать объекты на графе так, что соотношение количеств в соседних узлах равно константе. Если посмотреть на наш граф, как на ось абсцисс, то распределение шариков будет выглядеть как экспонента; вернее, как проекция экспоненты на дискретную решетку, причем каждое из значений экспоненты на решетке округлено до целого значения. В двух случаях, когда волна стабилизируется, этими экспонентами являются 1k и τk. Рассмотрим общий случай qk, q€R.
Без ограничения общности можно принять, что количество в 0-м узле равно 1. Начальное расположение на антенне и мат. ожидание расположения после первого шага выглядят, как показано на рис.1.
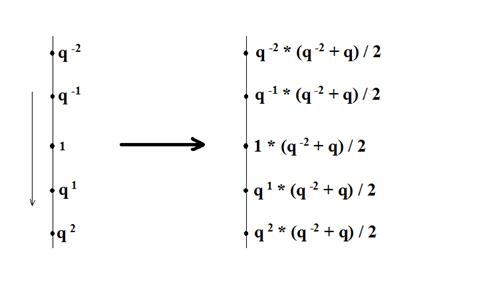
Рис. 1
Как видим, отношение количеств в соседних узлах после каждого шага сохраняется, остается равным q. Посмотрим, как ведет себя процесс X(t). Исследуем мат. ожидание приращения процесса:
E(X(2) - X(1)) = ½ (q-2 + q) – 1
обозначим
S = ½ (q-2 + q):
E(X(2) - X(1)) = S – 1 = δ1
Так как отношение количеств q после каждого шага сохраняется, S также не зависит от номера шага.
В рассмотренной формуле для приращений мы полагали, что в 1-й момент количество в 0-м узле равно 1. Для того, чтобы написать такую же формулу для следующего шага, нужно каждый член выражения домножить на S. Таким образом, приращения δ t связаны следующим соотношением:
δ t+1 = S δ t , (**)
то есть последовательность приращений представляет собой геометрическую прогрессию; последовательность мат. ожиданий процесса EX(t) – сумму геометрической прогрессии, а именно:
EX(t) = 1 + ∑ δ i , i =1, … , t-1
По формуле суммы геометрической прогрессии:
EX(t) = 1 + ∑ δ i = 1 + δ1 (1 – S
t-1)/(1 – S) = 1 + (S – 1) * (1 – S t-1)/(1 – S) = S t-1
.
Пусть в начальный момент времени в 0-м узле находится N0 шариков. Тогда:
EX(t) = N0 * S t - 1 . (***)
Примечание: эту формулу можно было получить и не рассматривая приращения, а просто исходя из постоянства отношения количеств в соседних узлах :) .
Обратимся к свойствам функции S(q) = ½ (q-2 + q) , q € (0, ∞).
Производная: S’(q) = ½ - q-3 ;
S’(q) = 0 при q0 = 21/3 ≈ 1.26 ;
S(q0) ≈ 0.945
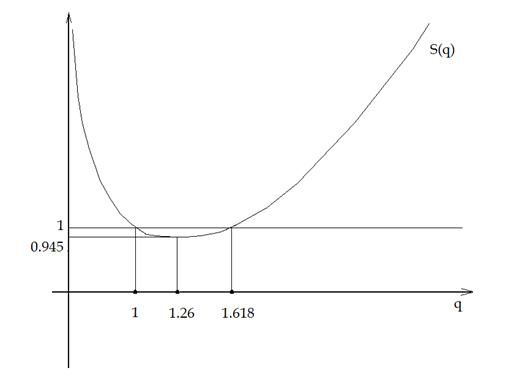
Рис. 2
График S(q) имеет две асимптоты: вертикальную, q=0 и наклонную, q/2.
Из формулы (***) вытекает, что процесс X(t) является возрастающим, когда S > 1 и убывающим, когда S < 1.
Вывод: Процесс стабилен, если входящий сигнал можно оценить как на экспоненту с основанием, «гуляющем» в интервале (1, τ).
См. также:
Самоподобные процессы
в коммуникативных сетях
Об одном методе моделирования самоподобного стохастического процесса