Колеблющееся
решение
(источник – Математическая энциклопедия)
Колеблющееся решение
–
решение дифференциального уравнения
обладающее
свойством: для любого t1 > t0 найдется точка t2
> t1, при переходе через которую функция x(t)меняет знак. Во
многих прикладных задачах возникает вопрос о существовании К. р. или о
колеблемости всех решений уравнения (*). Известно много достаточных условий, при
к-рых уравнение (*) имеет К. р. (см. [1] - [3]). Например, любое нетривиальное
решение уравнения х"+2dx' + w2 х = 0 с постоянными
коэффициентами колеблется, если d2<w2; любое
нетривиальное решение уравнения
с
w-периодическими коэффициентами колеблется, если
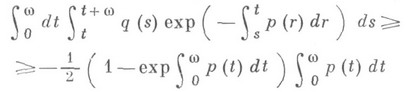
и 
на [0, w].
В ряде
приложений возникает вопрос о К. р. (в определенном смысле) системы
обыкновенных дифференциальных уравнений. Например, в теории регулирования
изучают колеблемость относительно заданной гиперплоскости 
решений х(t) = (x1(t),..., xn(t))
системы уравнений x' = f{t, x), т. е. вопрос о колеблемости функции. Изучают
также [a, b]-колеблющиеся 
решения, при этом ограниченное решение x(t)системы
х' = f(t, x) наз. [a, b]-колеблющимся, если функция s(t) колеблется и для
любого 
найдутся точки t2 и t3
такие, что tl < t2 < t3, s(t2)
< a, s(t3) > b, причем a < 0 < b. Для системы (2) существуют
и другие определения колеблемости решений.
Литература:
[1] Xартман
Ф., Обыкновенные дифференциальные уравнения, пер. с англ., М., 1970;
[2] Swansоn
С. А., Comparison and oscillation theory of linear differential equations, N. Y.-
L., 1968;
[3] Кигурадзе
И. Т., Некоторые сингулярные краевые задачи для обыкновенных дифференциальных
уравнений, Тб., 1975.