Операции с матрицами на C++. Класс DMatrix
Singular
distributions, dimension of support, and symmetry of Fourier transform
( Сингулярные распределения,
размерность носителя и симметричность преобразования Фурье )
Gady Kozma, Alexander Olevskii
2011
В статье рассмотрена симметрия Фурье мер и распределений в круге и ее связь с размером их носителей.
Главные результаты:
1. Одностороннее расширение теоремы Фростмана, устанавливающее связь между, с одной стороны, скоростью затухания преобразования Фурье некоторого распределения и, с другой стороны, размерностью Хаусдорфа носителя;
2. Построение компактов «критического» размера, на которых задаются распределения (в том числе – псевдо-функции) с неаналитической частью, принадлежащей к множеству l2.
Приведены примеры несимметричности, возникающей у мер с «маленьким» носителем. Сформулированы основные вопросы, оставшиеся открытыми.
I
Пусть K – компактное подмножество циклической группы T. Теорема Фростмана позволяет определить размерность Хаусдорфа множества K, исследуя невырожденные меры, для которых K является носителем.
Вот наиболее распространенный способ записи этой теоремы:
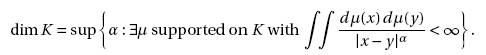
Нетрудно перевести это утверждение на язык коэффициентов Фурье:
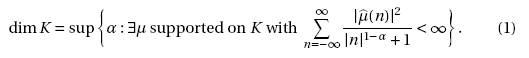
A. Beurling показал, что можно заменить меры на произвольные распределения (Шварца).
В этом случае мы получаем следующую версию теоремы Фростмана:
Теорема A.
Пусть 0 < α ≤ 1. Тогда:
(i) Если для невырожденного распределения S, у которого K является носителем, выполняется

то dim K
≥ α .
(ii) Если dim K > α, то существует вероятностная мера S, удовлетворяющая (2).
Покажем, что односторонняя оценка
![]() вполне достаточна для утверждения (i).
вполне достаточна для утверждения (i).
Теорема 1.
Пусть S – невырожденное распределение Шварца, для которого K является носителем и

тогда dim K ≥ α .
Обозначим D* пространство распределений Шварца и D* (K) - пространство распределений Шварца, для которого некоторый компакт K является носителем.
Следствие.
Если существует S € D* (K), такое, что ![]() , то dim K ≥
α .
, то dim K ≥
α .
… … … … …