О разрешимости дробно-линейных
дифференциальных уравнений в банаховых
пространствах.
(перевод Марата
Валиева)
Опишем множество начальных данных в абстрактной задачи Коши
для линейных
уравнений с дробной производной Капуто и неограниченным линейным замкнутым оператором
в банаховом пространстве X.
![]()
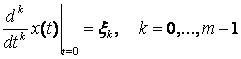
для которого соответствующие решения могут быть представлены
через функцию оператора Миттаг-Леффлера.
1.
Введение
Обыкновенные и частные уравнения дифференциального
порядка (с дробными производными Капуто, Римана-Лиувилля) разбудили в последние годы значительный интерес как в
математике, так и в приложениях. В математических трактатах по
дробно-дифференциальным уравнениям подход Римана-Лиувилля
к понятию дробной производной порядка ![]() обычно
используется так:
обычно
используется так:
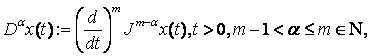 (1)
(1)
где
 (2)
(2)
![]()
дробный
интеграл Римана-Лиувилля порядка ![]() . Дробная производная Римана-Лиувилля
левая обратная (и не правая обратная) к соответствующему дробному интегралу,
который является естественным обобщением
формулы Коши для
. Дробная производная Римана-Лиувилля
левая обратная (и не правая обратная) к соответствующему дробному интегралу,
который является естественным обобщением
формулы Коши для ![]() й первообразной функции
й первообразной функции ![]() В
формулировании начального значения проблемы для обыкновенных (или задачи Коши
для частных) дифференциальных уравнений дробного порядка
В
формулировании начального значения проблемы для обыкновенных (или задачи Коши
для частных) дифференциальных уравнений дробного порядка ![]() с дробными
производными в форме Римана-Лиувилля, начальные
условия даны в терминах дробных интегралов
с дробными
производными в форме Римана-Лиувилля, начальные
условия даны в терминах дробных интегралов ![]() С другой
стороны, в области моделирования реальных процессов начальные условия, как
правило, выражаются через заданное число ограниченных начальных значений, принимаемых
переменной
С другой
стороны, в области моделирования реальных процессов начальные условия, как
правило, выражаются через заданное число ограниченных начальных значений, принимаемых
переменной ![]() и ее
производных целого порядка. В целях удовлетворения физических требований Капуто ввел альтернативное определение дробно-дифференциальной
производной. Оно было принято Капуто и Маинарди в рамках теории линейной вязкоупругости:
и ее
производных целого порядка. В целях удовлетворения физических требований Капуто ввел альтернативное определение дробно-дифференциальной
производной. Оно было принято Капуто и Маинарди в рамках теории линейной вязкоупругости:
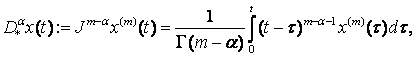 (3)
(3)
![]()
В некоторых издания
производная Капуто при ![]() была названа регуляризованной дробной производной порядка
была названа регуляризованной дробной производной порядка ![]() .
.
Используя идеи, связанные с теорией первого и второго
порядка абстрактных дифференциальных уравнений, некоторые результаты были
получены для абстрактной задачи Коши для дробно-линейного дифференциального
уравнения
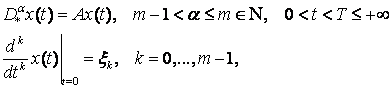 (4)
(4)
где
![]() линейный неограниченный замкнутый оператор в банаховом пространстве
линейный неограниченный замкнутый оператор в банаховом пространстве ![]() . В статьях [2],[9] были даны необходимые и
достаточные условия разрешимости задачи Коши (4) при условии
. В статьях [2],[9] были даны необходимые и
достаточные условия разрешимости задачи Коши (4) при условии ![]() , расширяя условия
теоремы Хилле-Йосида от
, расширяя условия
теоремы Хилле-Йосида от ![]() до
до ![]() . Условие
. Условие ![]() было посчитано в [4]. В статье [10] были получены условия
разрешимости при
было посчитано в [4]. В статье [10] были получены условия
разрешимости при ![]() для абстрактной задачи Коши (4) с дробной производной Римана-Лиувилля вместо
производной Капуто и начальных условий, данных в терминах дробных интегралов
для абстрактной задачи Коши (4) с дробной производной Римана-Лиувилля вместо
производной Капуто и начальных условий, данных в терминах дробных интегралов ![]() .
.
Другой, эквивалентный подход к задаче (4) состоит в
сужении данной задачи на преобразованное интегральное уравнение вида:
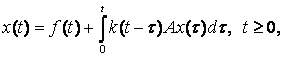 (5)
(5)
где
![]() скалярное ядро.
Общая теория таких уравнений (так же при не скалярном
условии, т.е.
скалярное ядро.
Общая теория таких уравнений (так же при не скалярном
условии, т.е. ![]() и оператор
и оператор ![]() зависит от
зависит от ![]() ) была представлена в [18]. Специальное условие для
ядра
) была представлена в [18]. Специальное условие для
ядра ![]() и
дифференциального оператора
и
дифференциального оператора ![]() первого порядка
для
первого порядка
для ![]() ,
второго порядка для
,
второго порядка для ![]() в Гильбертовом пространстве
было посчитано подробно в [4],[20].
Последняя статья так же содержит исследования численных методов для этой
задачи.
в Гильбертовом пространстве
было посчитано подробно в [4],[20].
Последняя статья так же содержит исследования численных методов для этой
задачи.
Известно, что если ![]() или
или ![]() ([12]) и
оператор
([12]) и
оператор ![]() может быть
представлен мультипликативной константой, единственное решение задачи Коши (4) для
может быть
представлен мультипликативной константой, единственное решение задачи Коши (4) для ![]() задается
формулой
задается
формулой
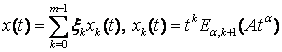 (6)
(6)
с обобщенной
функцией Миттаг-Леффлера заданной через
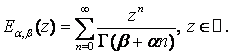 (7)
(7)
Частные решения ![]() так же могут
быть представлены в виде ([6],[12])
так же могут
быть представлены в виде ([6],[12])
![]()
где
![]()
![]() -кратный
интеграл (заменяя
-кратный
интеграл (заменяя ![]() на
на ![]() в (2)) и
в (2)) и
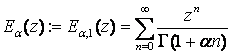 (8)
(8)
классическая
функция Миттаг-Леффлера.
Пусть теперь ![]() будет общим банаховым пространством и
будет общим банаховым пространством и ![]() будет линейным неограниченным
замкнутым оператором на пространстве
будет линейным неограниченным
замкнутым оператором на пространстве ![]() . Используя методы данные в [1], [16] при
. Используя методы данные в [1], [16] при ![]() , мы опишем начальные условия задачи Коши (4), для которых
решения могут быть так же представлены в виде (6). Это описание дано в терминах так называемых пространств Румье,
порожденных оператором
, мы опишем начальные условия задачи Коши (4), для которых
решения могут быть так же представлены в виде (6). Это описание дано в терминах так называемых пространств Румье,
порожденных оператором ![]() и их
индуктивными и проективными пределами, пространств Жеврея
и Берлинга.
и их
индуктивными и проективными пределами, пространств Жеврея
и Берлинга.
2. Линейные
уравнения дробного порядка.
В условии неограниченного оператора ![]() правая часть
отношения (6) не определено на всем Банаховом
пространстве
правая часть
отношения (6) не определено на всем Банаховом
пространстве ![]() . Однако мы можем исследовать условия для
. Однако мы можем исследовать условия для ![]() под которыми,
зависящий от времени оператор
под которыми,
зависящий от времени оператор ![]() где
где
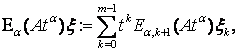 (9)
(9)

корректно
определена. Мы будем называть оператор ![]() данный в (9)
так же, как и оператор-функцию Миттаг-Леффлера.
данный в (9)
так же, как и оператор-функцию Миттаг-Леффлера.
Докажем, что для каждого ![]() формула (9)
определяет решение задачи Коши (4). Описание множества начальных значений, для
которых задача Коши (4) имеет решение в виде (9), может быть дано в терминах
пространств Румье, созданных оператором
формула (9)
определяет решение задачи Коши (4). Описание множества начальных значений, для
которых задача Коши (4) имеет решение в виде (9), может быть дано в терминах
пространств Румье, созданных оператором ![]() . (см. [1], [5], [16]).
. (см. [1], [5], [16]).
О п р е д е л е н и е 2.1. Пусть ![]() линейный
неограниченный оператор в Банаховом пространстве
линейный
неограниченный оператор в Банаховом пространстве ![]() последовательность с
последовательность с ![]() , и
, и ![]() . Пространство Румье
. Пространство Румье ![]() определим как
множество элементов
определим как
множество элементов ![]() , таких, что
, таких, что
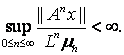
Оснащенное
нормой
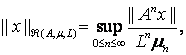 (10)
(10)
это
пространство – Банахово пространство, непрерывно
вложенное в пространство ![]() .
.
Так же мы будем использовать пространства Берлинга и Жеврея
![]()
Эти пространства оснащены топологиями индуктивных и
проективных пределов, соответственно, локально выпуклых пространств.
Одной из самых важных проблем в теории пространств Румье, Берлинга и Жеврея связанных с абстрактной задачей Коши для
дифференциальных уравнений дробного порядка является проблема плотности этих
пространств в пространстве ![]() . Для обзора
некоторых результатов в классическом случае
. Для обзора
некоторых результатов в классическом случае ![]() см., например, в работе [1]. Надо заметить, что наиважнейшие результаты в этом направлении были
выведены для условий
см., например, в работе [1]. Надо заметить, что наиважнейшие результаты в этом направлении были
выведены для условий ![]() Мало чего может
быть найдено при условии
Мало чего может
быть найдено при условии ![]() , и оно должно быть еще исследовано.
, и оно должно быть еще исследовано.
В этой статье мы будем иметь дело с пространствами Румье с последовательностью ![]() которое обозначим как
которое обозначим как ![]() . Связь этих пространств с классическими
пространствами Румье
. Связь этих пространств с классическими
пространствами Румье ![]() с
с ![]() дана в
следующем простом результате.
дана в
следующем простом результате.
Л е м м
а 2.1. Вложения
![]()
остаются
верными для ![]() и для каждого
и для каждого ![]() , если
, если ![]() .
.
Д о к а з а т е л ь с т в о. Условие ![]() очевидно. Для
очевидно. Для ![]() , используя асимптотическую
формулу Стирлинга для гамма функции (см. например [15]), мы получим оценку
, используя асимптотическую
формулу Стирлинга для гамма функции (см. например [15]), мы получим оценку
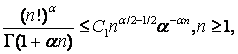
с
константой ![]() , зависящей от
, зависящей от ![]() . Эта оценка влечет вложения
(11) и (12):
. Эта оценка влечет вложения
(11) и (12):
![]() (11)
(11)
![]() (12)
(12)
![]() Соединяя
(11) и (12) мы получим утверждение Леммы 2.1.
Соединяя
(11) и (12) мы получим утверждение Леммы 2.1.
Как прямое следствие предыдущей леммы и определения
пространств Берлинга и Жеврея
мы получим следующий результат:
Л е м м
а 2.2. Для пространств Берлинга и Жеврея ![]() образованных
семействами множеств Румье
образованных
семействами множеств Румье ![]() и
и ![]() , соответственно имеют место тождества
, соответственно имеют место тождества
![]() (13)
(13)
Опишем множество начальных данных задачи Коши (4) в банаховом
пространстве X, для которых решения
могут быть представлены в виде (9). Мы сделаем это в терминах пространства Румье ![]() , порожденных оператором А.
, порожденных оператором А.
Т е о р
е м а 2.1. Пусть А
– линейный неограниченный замкнутый
оператор в Банаховом
пространстве Х и ![]() .
.
Если
решение (9) задачи Коши (4) существует на
отрезке ![]() , тогда
, тогда ![]() для каждого
для каждого ![]() .
.
Наоборот,
если для некоторого ![]() ,
, ![]() , тогда оператор-функция Миттаг-Леффлера
данная в (9) определяет решение задачи Коши (4) на интервале
, тогда оператор-функция Миттаг-Леффлера
данная в (9) определяет решение задачи Коши (4) на интервале ![]() .
.
Д о к а з а т е л ь с т в о. Пусть функция
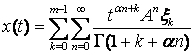
с фиксированными ![]() будет
определена на интервале
будет
определена на интервале ![]() . Тогда
. Тогда

и, следовательно,
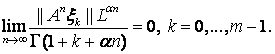
Используя асимптотическую формулу [15]
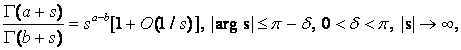 (14)
(14)
мы приходим к каждому ![]() в отношении
в отношении
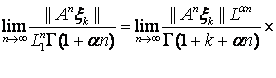
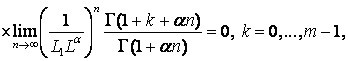
которое влечет включение ![]()
Обратно, пусть ![]() Начиная
с
Начиная
с ![]() ряды
ряды
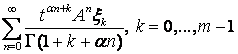
абсолютны и равномерны на каждом компакте интервала ![]() . Следовательно эти ряды для
каждого фиксированного
. Следовательно эти ряды для
каждого фиксированного ![]() определяют
линейный оператор (обозначим его как
определяют
линейный оператор (обозначим его как ![]() ) из
) из ![]() в
в ![]() . Если зафиксируем элемент
. Если зафиксируем элемент ![]() , тогда функция
, тогда функция
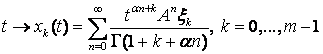 (15)
(15)
непрерывна
на интервале ![]() . Так же мы имеем
. Так же мы имеем
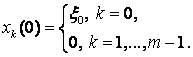
Докажем теперь, что ![]() .
Действительно, обычным дифференцированием (15) мы получим ряды
.
Действительно, обычным дифференцированием (15) мы получим ряды
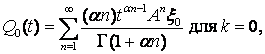
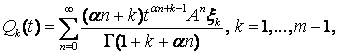
которые
абсолютны и равномерны на каждом компактном подмножестве интервала ![]() (
(![]() в случае
в случае ![]() ). Следовательно
). Следовательно ![]() , и
, и ![]() для всех
для всех ![]() . В случае
. В случае ![]() мы можем
непосредственно проверить, что
мы можем
непосредственно проверить, что

Повторяя те же выкладки ![]() раз и используя
формулу
раз и используя
формулу
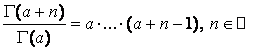
мы придем к
выражению
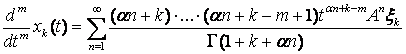 (16)
(16)
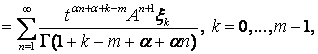
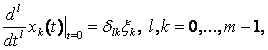
и включение ![]() Начиная
с
Начиная
с ![]() , все функции
, все функции 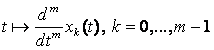 интегрируемы на
интервале
интегрируемы на
интервале ![]() .
.
Используя формулу
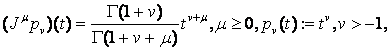
и выражение (16) мы получим ![]()
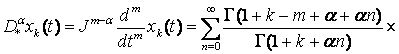
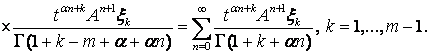
С другой стороны, так как оператор ![]() замкнут, мы
получим
замкнут, мы
получим
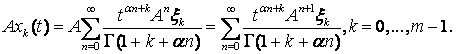
![]() Суммируя
полученные результаты, мы увидим, что оператор-функция (9) определяет решение
задачи Коши (4) на интервале
Суммируя
полученные результаты, мы увидим, что оператор-функция (9) определяет решение
задачи Коши (4) на интервале ![]()
С л е д с т в и е 2.1. Утверждение Теоремы 2.1 может быть переписано в терминах пространств
Жеврея и Берлинга. А
именно, функция оператора Миттаг-Леффлера (9)
определяет решение задачи Коши (4) на
подходящем интервале ![]() (на каждом
интервале
(на каждом
интервале![]() ) тогда и только тогда, когда
) тогда и только тогда, когда ![]()
3.
Функция оператора Миттаг-Леффлера.
Рассмотрим теперь некоторые свойства функции оператора Миттаг-Леффлера ![]() данной в
(9). Для простоты мы ограничимся
условием
данной в
(9). Для простоты мы ограничимся
условием ![]() . При этом условии (зафиксируем
. При этом условии (зафиксируем ![]() как
как ![]() ) (9) переходит в
) (9) переходит в
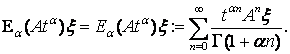 (17)
(17)
Т е о р
е м а 3.1. Пусть ![]() линейный
неограниченный замкнутый оператор в Банаховом пространстве
линейный
неограниченный замкнутый оператор в Банаховом пространстве ![]()
Тогда
правая сторона отношения (17) определяет, при ![]() , непрерывный линейный оператор
, непрерывный линейный оператор ![]() , действующий из
, действующий из ![]() в
в ![]() с оценкой нормы
с оценкой нормы
 (18)
(18)
Д о к а з а т е л ь с т в о. Для ![]() неравенство
неравенство ![]() остается верным
(число
остается верным
(число ![]() дано в Теореме
3.1). Тогда, основываясь на доказательство Теоремы 2.1,
дано в Теореме
3.1). Тогда, основываясь на доказательство Теоремы 2.1, ![]() для
для ![]() Кроме
того, что мы докажем, что оператор
Кроме
того, что мы докажем, что оператор ![]() действует из
пространства
действует из
пространства ![]() в пространство
в пространство ![]() с нормой,
оцененной (18). Мы используем вспомогательное
неравенство
с нормой,
оцененной (18). Мы используем вспомогательное
неравенство
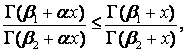 если
если ![]() (19)
(19)
которое
является простым следствием теоремы суммирования Гаусса для гипергеометрических
функций ![]() ([15]):
([15]):
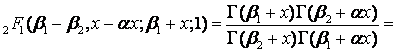
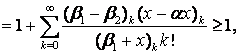
где ![]() означает символ
Похгаммера. Докажем (18). Используя неравенство (19), биномиальные ряды
означает символ
Похгаммера. Докажем (18). Используя неравенство (19), биномиальные ряды
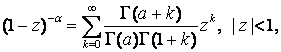
неравенство (![]()
![]() (20)
(20)
следующее из (10), и некоторые элементарные оценки,
получим
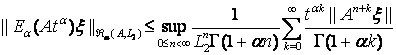
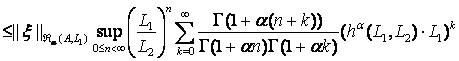
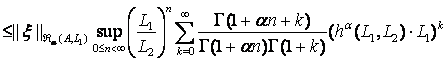
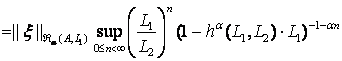
![]()
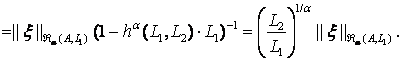
З а м е ч а н и е 3.1. В
специальном условии ![]() мы имеем
мы имеем 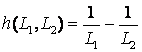 и оценкой нормы
(18) в виде
и оценкой нормы
(18) в виде
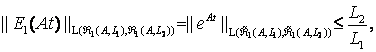
которая в
соответствии с результатами работы [1]. Если ![]() , тогда
, тогда ![]() для всех
фиксированных
для всех
фиксированных ![]() с
с ![]()
Т е о р
е м а 3.2. Пусть ![]() линейный
неограниченный замкнутый оператор в Банаховом
пространстве
линейный
неограниченный замкнутый оператор в Банаховом
пространстве ![]() и
и ![]()
Тогда
оператор-функция Миттаг-Леффлера ![]() заданная в (17)
– непрерывный линейный оператор, действующий из
заданная в (17)
– непрерывный линейный оператор, действующий из ![]() в
в ![]() для всех
для всех ![]() , и
, и
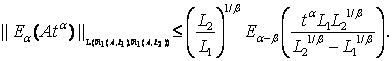 (21)
(21)
Д о к а з а т е л ь с т в о. Нам понадобятся два
вспомогательных неравенства
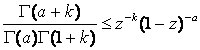 для всех
для всех ![]() (22)
(22)
и
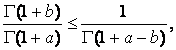 для всех
для всех ![]() (23)
(23)
Для доказательства первого неравенства мы заметим, что ![]()
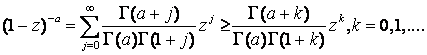
Используя теорему суммирования Гаусса для
гипергеометрических функций ![]() , мы получим
, мы получим ![]()
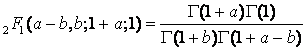
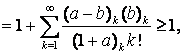
что и доказывает (23). Теперь пусть ![]() и
и ![]() . Используя неравенства (19), (20), (22) (с
. Используя неравенства (19), (20), (22) (с ![]() ) и (23), мы имеем
) и (23), мы имеем
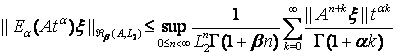
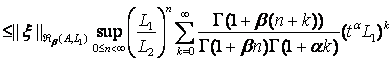
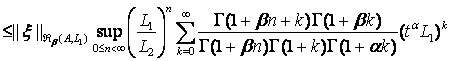
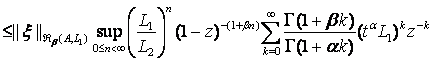
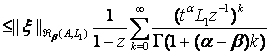
![]()
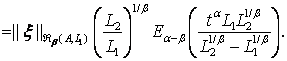
Список литературы
[1]
E. A. B a r k o v a, P. P. Z a b r e j k o, On the
solvability of linear
differential
equations with unbounded operators in Banach spaces. ZAA
17
(1998),
339-360.
[2]
E. B a z h l e k o v a, The abstract Cauchy problem
for the fractional
evolution
equation. Fractional Calculus & Applied Analysis 1 (1998),
255-
270.
[3]
M. C a p u t o, Linear models of dissipation whose Q is almost frequency
independent,
Part II. Geophys. J. R. Astr. Soc. 13
(1967), 529-539.
[4]
A. M. A. E l - S a y e d, Fractional order evolution equations. Journal of
Fractional
Calculus 7 (1995),
89-100.
[5]
I. M. G e l’ f a n d , G. E. S h i
l o v, Generalized Functions, Vol. 2: Spaces
of
Basic and Generalized Functions. Moscow, Fizmatgiz (1958).
[6]
R. G o r e n f l o, F. M a i n a r d i, Fractional calculus: integral and
differential
equations of fractional order. In: Fractals and fractional calculus
in
continuum mechanics (Eds. A. Carpinteri and F. Mainardi). Wien
and
New
York, Springer Verlag (1997), 223-276.
[7]
R. G o r e n f l o, F. M a i n a r d i, Random walk models for space-fractional
diffusion
processes. Fractional Calculus and Applied Analysis 1 (1998), 167-
191.
[8]
V. K i r y a k o v a, Generalized Fractional
Calculus and Applications,
Pitman Research Notes in Math., Vol.
301. Harlow, Longman (1994).
[9]
A. N. K o c h u b e i, A Cauchy problemfor
evolution equations of fractional
order.
Differ. Equations 25 (1989), 967-974.
[10]
V. A. K o s t i n, The Cauchy problem for an abstract
differential equations
with
fractional derivatives. Russian Acad. Sci. Dokl. Math. 46
2 (1993), 316-
319.
[11]
Yu. L u c h k o, R. G o r e n f l o, Scale-invariant solutions of a partial
differential
equation
of fractional order. Fractional Calculus & Applied Analysis 1
1
(1998), 49-63.
[12]
Yu. L u c h k o, R. G o r e n f l o, An operational
method for solving fractional
differential
equations with the Caputo derivatives. Acta
Mathematica
Vietnamica, to appear.
[13]
Yu. F. L u c h k o, H. M. S r i v a s t a v a, The exact solution of certain
differential
equations of fractional order by using operational calculus.
Comput.
Math. Appl. 29
(1995), 73-85.
[14]
F. M a i n a r d i, Fractional calculus: some basic problems in continuum
and
statistical mechanics. In: Fractals and Fractional Calculus in Continuum
Mechanics (Eds.
A. Carpinteri, F. Mainardi).
Wien and New York, Springer
Verlag
(1997), 291-348.
[15]
O. I. M a r i c h e v, Handbook of Integral
Transforms of Higher Transcendental
Functions, Theory and Algorithmic Tables.
Chichester, Ellis Horwood
(1983).
[16]
V. I. N a z a r o v, Solvability of linear differential equations in scales of
Roumieu spaces defined by a linear unbounded
operator. Diff. Uravn.
26
(1990),
1598-1608.
[17]
I. P o d l u b n y, Fractional Differential Equations, Mathematics in
science
and
engineering, Vol. 198. New York, Academic Press (1999).
[18]
J. P r ¨u s s, Evolutionary Integral Equations
and Applications. Basel,
Birkh¨auser (1993).
[19]
S. G. S a m k o, A. A. K i l b a s and O. I. M a r i c h e v, Fractional
Integrals
and Derivatives: Theory and Applications.
New York, London, and
Paris, Gordon and Breach (1993).
[20]
G. W i t t e, Die analytische und die numerische Behandlung einer Klasse
von
Volterraschen Integralgleichungen
im Hilbertraum.
Berlin, Logos Verlag
(1997).