Операции с матрицами на C++. Класс DMatrix
Системы счисления, основанные на Золотой пропорции.
Система счисления Стахова + программа - демонстратор
Избыточные недвоичные системы счисления *
J.T. Butler, T.Sasao
( Оригинал статьи на английском:
Redundant Multiple-Valued Number Systems )
ПРЕДИСЛОВИЕ
В данной статье мы рассмотрим
системы счисления, использующие цифры
больше единицы и допускающие избыточность в представлении чисел. К
избыточным относятся системы счисления, в которых одно и то же число может быть
представлено как минимум двумя способами. В качестве эталона для сравнения
будем рассматривать обычную двоичную систему счисления. Сравнивать системы мы
будем по степени избыточности, то есть – по тому, сколько существует избыточных
представлений.
ВВЕДЕНИЕ
В
человеческом обществе принято обменивать продукт труда одного типа на продукт
труда другого типа. Например, когда человек расплачивается в ресторане, он
обменивает деньги, полученные от своей трудовой деятельности, на результат
работы поваров, скотоводов, земледельцев, транспортников и т.д. Такой обмен
возможен благодаря существованию расценок на те или иные результаты труда. Существует много способов выразить эту
величину. Однако практически у всех систем счисления для представления
различных чисел используется комбинация конечного набора символов. Десятичная
система счисления распространена наиболее широко; принято считать, что это
связано с количеством пальцев на руках. Аналогичная ситуация существует и в
сфере компьютерной техники: так как проще всего построить логические элементы,
имеющие два состояния, в компьютерах используется двоичная система. Обзор
публикаций по многозначной логике позволяет сделать вывод о перспективности систем счисления,
использующих цифры больше единицы.
Несмотря
на то, что двоичные системы получили широкое распространение только в настоящее
время, существуют данные о том, что в
Китае использовали двоичные системы еще 5000 лет назад (Newman [15, p. 2422]).
Интересное
исследование было проведено на раскопках Mohenjo-Daro, античного города, расположенного
недалеко от реки Инд (Morrison
and
Morrison
[14]). Были обнаружены камни неправильной формы, отличающиеся друг от друга по
весу как 2n
. Археологи считают, что они использовались торговцами культуры Harappan в
качестве гирь для рычажных весов 4000 лет назад. Предмет взвешивался с помощью этого набора
камней, и таким образом его вес мог быть последовательно записан в двоичной
системе счисления. Рычажные весы изображены на Рис 1.
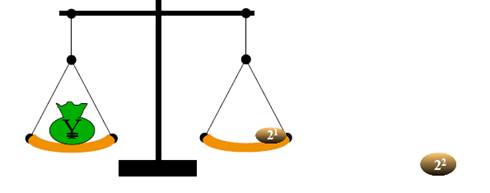
Рис.1
Принцип
работы такой системы прост: сначала находятся два маленьких камня с одинаковым
весом; для установления их идентичности используются весы. Любопытно, что на
раскопках обнаружены два камня с весами, отличающимися менее чем на унцию.
Затем, опять используя те же весы, находится третий камень, равный по весу
сумме двух предыдущих. Эти три камня используются для поиска четвертого, снова
равного по весу сумме предыдущих, и так далее. Таким образом, вес камней
определяется последовательностью: 1, 1,
2, 4, 8, 16, ... .
СРАВНЕНИЕ
СИСТЕМ СЧИСЛЕНИЯ
СТАНДАРТНАЯ ДВОИЧНАЯ СИСТЕМА
В стандартной
двоичной системе счисления представление числа N определяется как
N = an-12n-1 + ... + a222 + a121 + a020, где ai Î {0, 1}.
На рис.2 приведен
пример стандартной двоичной системы с резолюцией 4 разряда. В таблице приведены
четырехразрядные двоичные представления и их значения. Гистограмма отображает
количество различных представлений для каждого числа: очевидно, что существует
одно и только одно 4-битное представление для каждого неотрицательного целого
от 0 до 15.
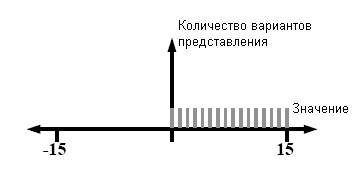
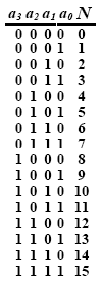
N = a323+a222+a121+a020, где ai
e {0,1}.
Рис. 2.
Стандартная четырехбитная система счисления
НЕГА-ДВОИЧНАЯ СИСТЕМА
В нега-двоичной
системе счисления можно представлять как положительные, так и отрицательные целые
числа. Представление здесь выглядит так же, как и в стандартной двоичной, но с
заменой основания «2» на «-2»:
N = an-1(-2)n-1 + ... + a2(-2)2 + a1(-2)1 + a0(-2)0
На рис.3
проиллюстрирована четырехбитная нега-двоичная система. Как и в стандартном случае,
каждое число имеет единственное представление. Интересно, что с помощью
определенного четного количества битов можно представить вдвое больше
отрицательных чисел, чем положительных. Если количество бит – нечетное,
количество положительных чисел больше, чем количество отрицательных, в два раза
+ 1. Такое несоответствие между количеством положительных и отрицательных чисел
очень неудобно.
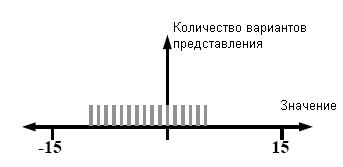

N = a3(-2)3+a2(-2)2+a1(-2)1+a0(-2)0, где ai
e {0,1}.
Рис. 3.
Нега-двоичная четырехбитная система счисления
СИСТЕМА С ДОПОЛНЕНИЕМ ДО ДВУХ
Как и в случае нега-двоичной
системы, система с дополнением до двух позволяет представлять и положительные,
и отрицательные целые числа. Однако, в этом случае количество положительных и
отрицательных чисел в пределе одинаково. Представление выглядит так:
N = an-1(-2)n-1 + ... + a222 + a121 + a020
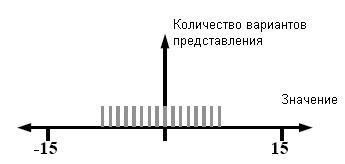
Рис.4
иллюстрирует четырехбитную систему с дополнением до двух. Как и во всех
предыдущих случаях, эти представления уникальны. В данной системе при заданном
количестве бит количество представимых отрицательных чисел на единицу больше,
чем положительных.

N = a3(-2)3+a222+a121+a020, где ai
e {0,1}.
Рис. 4. Система
счисления с дополнением до двух, четырехбитная
СИСТЕМА С ДОПОЛНЕНИЕМ ДО ЕДИНИЦЫ
Данная система –
первый пример избыточной системы счисления. Действительно, число 0 имеет два
представления, обозначаемые здесь как «0» и «-0». Каждое число представляется в
этой системе как
N = an-1(-2)n-1 + ... + a222 + a121 + a020 + an-1 ;
число «0» - это 00…0, а число
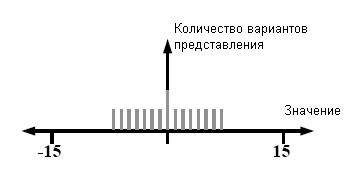
«-0» - 11…1 . На рис.5 изображена
четырехбитная система с дополнением до единицы. Двойственность представления нуля
показана линией двойной амплитуды в точке 0.
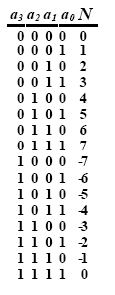
N = a3(-2)3+a222+a121+a020 +a3, где ai
e {0,1}.
Рис. 5. Система счисления с дополнением до единицы, четырехбитная
СИСТЕМА СЧИСЛЕНИЯ ФИБОНАЧЧИ
Система
счисления Фибоначчи является следующим примером избыточной системы. В данной
системе каждое число представляется как
N = an-1Fn+1 +
... + a2F4
+ a1F3 + a0F2 ,
где Fi = Fi-1 + Fi-2 и F2 = F1 = 1.
Таким образом,
вместо степеней 2 или -2 в качестве основания используются числа Фибоначчи. В
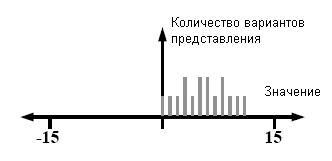
этой системе присутствует много избыточных представлений. На рис.6 показано,
что в четырехбитной системе Фибоначчи их четыре.

N = a3F5 + a2F4 + a1F3 + a0F2, где ai e {0,1} and Fi
– i-е число Фибоначчи,
то есть: N = a3*5 + a2*3 + a1*2 + a0.
Рис. 6. Система
счисления Фибоначчи, четырехбитная
СИСТЕМА ФИБОНАЧЧИ БЕЗ СМЕЖНЫХ
ЕДИНИЦ
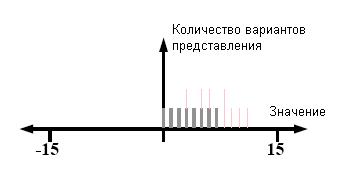
Цекендорф [16]
доказал, что любое целое число может быть записано как сумма чисел Фибоначчи и такое представление единственно, если
не содержит двух единиц подряд. (см. рис.7). В таблице ниже вычеркнуты строки
со смежными единицами. Таким образом, с помощью четырехбитной системы можно
однозначно представить числа от 0 до 7.
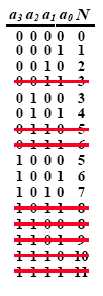
N = a3F5 + a2F4 + a1F3 + a0F2, где ai e {0,1} and Fi
– i-е число Фибоначчи,
то есть: N = a3*5 + a2*3 + a1*2 + a0.
Рис. 7.
Система счисления Фибоначчи без смежных единиц, четырехбитная
Отсутствие
рядом стоящих единиц делает эту систему удобной для систем с последовательным
доступом и хранением данных. Например, Davies [6]
описывает подобную систему для работы с CD-ROM, в которой использованы кодовые
слова без пар единиц. Kautz
[12] предложил коды, которые могут передаваться без сигнала синхронизации, при
условии, что есть достаточно переходов из 0 в 1 и из 1 в 0 для того, чтобы
определить, где битовая строка начинается и заканчивается.
СИСТЕМА ФИБОНАЧЧИ С ДОМИНИРОВАНИЕМ
ЕДИНИЦ
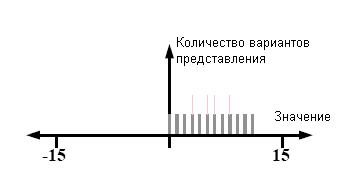
Brown [1] доказал, что, исключая в системе Фибоначчи
представления с двумя нулями подряд, можно записать любое число единственным образом.
Иначе говоря, представление Фибоначчи, в котором единиц больше, чем нулей,
является уникальным. На рис.8 изображен четырехбитный случай.

N = a3F5 + a2F4 + a1F3 + a0F2, где ai e {0,1} и Fi – i-е число Фибоначчи,
то есть: N = a3*5 + a2*3 + a1*2 + a0.
Рис. 8.
Система счисления Фибоначчи с доминированием единиц, четырехбитная
СИСТЕМА НЕГА-ФИБОНАЧЧИ
Следующий вариант системы Фибоначчи позволяет
представлять как положительные, так и отрицательные целые числа. Пусть F-i = (-1)i+1Fi
и
N = an-1F-(n+1) + ... + a2 F-4 + a1
F-3 + a0 F-2,
где ai Î {0,1}
и Fi – числа
Фибоначчи
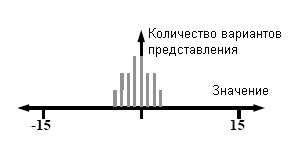
N принимает отрицательное значение, если сумма отрицательных чисел
Фибоначчи в представлении превышает сумму положительных. На рис. 9 приведены
представления для n≤4. Заметим, что эта система – весьма избыточная.

N = a3F-4 + a2F-3 + a1F-2 + a0F-1,
где ai
e {0,1} и F-i= (-1)i+1Fi for Fi
– i-е число Фибоначчи, то есть
N = a3*(-3) + a2*2 + a1*(-1) + a0.
Рис. 9.
Система нега-Фибоначчи, четырехбитная
СИСТЕМА НЕГА-ФИБОНАЧЧИ БЕЗ СМЕЖНЫХ
ЕДИНИЦ
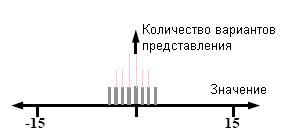
В статье [3] Bunder показал, что после исключения в системе нега-Фибоначчи
представлений, содержащих две единицы подряд, оставшиеся представления будут
уникальными. На рис.10 показано, что для четырехбитной системы останется 8
представлений для чисел от -4 до 3.

N = a3F-4 + a2F-3 + a1F-2 + a0F-1,
где ai
e {0,1}, F-i=
(-1)i+1Fi и Fi
- i-е число Фибоначчи.
N = a3*(-3) + a2*2 + a1*(-1) + a0.
Рис. 10.
Система нега-Фибоначчи без смежных единиц, четырехбитная
СИСТЕМА ТРИБОНАЧЧИ
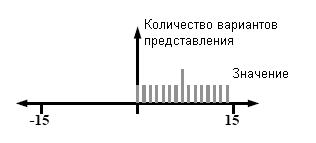
Естественным развитием системы Фибоначчи является система
трибоначчи, см. Capocelli и соавторы [5] и
Fraenkel [8]. В этой системе число представляется
в виде:
N = an-1Fn+1 + ... + a2 F4 + a1
F3 + a0 F2,
где Fi = Fi-1
+ Fi-2 + Fi-3, F4 = 22, F3 = 21 и F2 = 20.

N = a3F5 + a2F4 + a1F3 + a0F2,
где ai e {0,1} и Fi – i-е число
трибоначчи, то есть:
N = a3*7 + a2*4 + a1*2 + a0.
Рис.
11. Система трибоначчи, четырехбитная
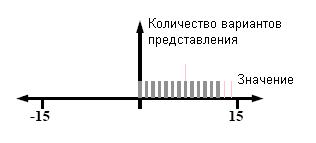
СИСТЕМА ТРИБОНАЧЧИ С ОГРАНИЧЕНИЕМ
В работе [8] Fraenkel, в частности, доказал, что после
исключения представлений с тремя или более единицами подряд оставшиеся представления
будут уникальными. Рис.12 иллюстрирует тот факт, что в четырехбитной системе Tрибоначчи, где три единицы подряд исключены, числа
0, 1, ... , 12 представлены однозначно.

N = a3F5 + a2F4 + a1F3 + a0F2,
где ai
e {0,1} and Fi
– i-е число трибоначчи, то есть:
N = a3*7
+ a2*4 + a1*2 + a0.
Рис.
12. Система Трибоначчи с ограничением, четырехбитная
Этот
результат можно обобщить. Действительно, в [8] доказано, что в системе
счисления, где Fi
задаются
формулой:
Fi = Fi-1 + Fi-2 + ... +Fi-m при i > m+1
и
Fi = 2i-2 при 1 < i
≤ m+1
и нет более чем m-1 идущих подряд единиц, представление
чисел уникально.
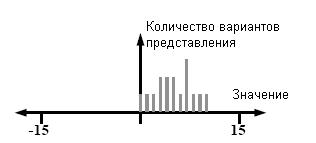
СИСТЕМА СЧИСЛЕНИЯ ФИБОНАЧЧИЕВОГО ТИПА
Следующее
естественное обобщение фибоначчиевой системы – система фибоначчиевого типа,
описанная Klein’ом
[13], в которой числа представлены в форме:
N = an-1Fn+1 + ... + a2 F4 + a1
F3 + a0 F2,
где Fi = Fi-1 +
Fi-m при i >
m+1 и
Fi = i-1 при 1 < i ≤
m+1, m ≥
2
Рис.13
иллюстрирует четырехбитную систему. Она избыточна и содержит 5 дублирующих
представлений.

N = a3F5 + a2F4 + a1F3 + a0F2,
где ai e {0,1}, Fi – i-е
число фибоначчиевого типа,
Fi = Fi-1 + Fi-3 & F4 =3, F3=2, & F2= 1
то есть: N = a3*4 + a2*3
+ a1*2 + a0.
Рис.
13. Система фибоначчиевого типа,
четырехбитная
СИСТЕМА ФИБОНАЧЧИЕВОГО ТИПА, В КОТОРОЙ
КАЖДАЯ ПАРА ЕДИНИЦ РАЗДЕЛЕНА ДВУМЯ ИЛИ БОЛЕЕ НУЛЯМИ
На основании теоремы 1 в статье Fraenkel’я [8] мы можем сделать следующий вывод.
Если каждая пара единиц разделена, как минимум, m-1
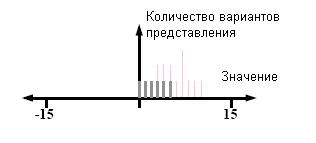
нулями, то представления чисел уникальны. На рис.14 показана четырехбитная
система такого типа, где числа 0, 1, ... , 5 представлены однозначно.
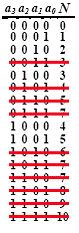
N = a3F5 + a2F4 + a1F3 + a0F2,
где ai e {0,1}, Fi – i-е число фибоначчиевого типа,
Fi = Fi-1 + Fi-3 & F4 =3, F3=2, & F2= 1
то есть: N = a3*4 + a2*3
+ a1*2 + a0.
Рис.
14. Четырехбитная система фибоначчиевого
типа, в которой каждая пара единиц разделена двумя или более нулями
СИСТЕМА m-НАЧЧИ
Следующий
вариант системы Фибоначчи – недвоичная система счисления, характеризующаяся
следующей формулой представления чисел:
N = an-1Fn+1 + ... + a2 F4 + a1
F3 + a0 F2,
где цифры при Fi - 0, 1, ... , m-1
и основание задано как Fi = m Fi-1 - Fi-2
при i >
3,
F3 = m, F2 =
1
и m ≥
3.
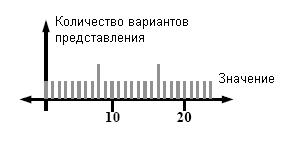
На рис.15 показана троичная система с m=3. В этом случае присутствуют две избыточных
записи.

N = a2F4 + a1F3 + a0F2, где ai
e {0,1,2} и Fi – i-е число m – наччи,
Fi = mFi-1 - Fi-2 , F3 = m & F2= 1, то
есть:
N = a2*8
+ a1*3 + a0 при m
= 3
Рис.
15. Троичная
m-наччи
система, где m=3
m-НАЧЧИ
СИСТЕМА, В КОТОРОЙ КАЖДАЯ ПАРА ЦИФР m-1 РАЗДЕЛЕНА КАК МИНИМУМ ОДНОЙ ЦИФРОЙ iÎ{0,1,...m-3}
Klein [13] показал, что если в системе m-наччи каждая пара цифр m-1
отделена как минимум одной i Î
{0,1,...m-3}, то каждое число имеет уникальное представление.
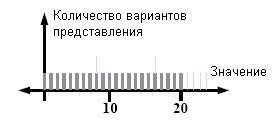
На рис.16 показано, что при таком условии 6 представлений на Рис.15 являются избыточными, после чего
остается 21 число, представленное уникально.
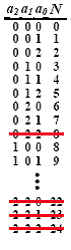
N = a2F4 + a1F3 + a0F2, где ai
e {0,1,2}, Fi –
i-е число m – nacci,
Fi = mFi-1 + Fi-2 , F3 = m & F2= 1, то
есть:
N = a2*8
+ a1*3 + a0 при m =
3.
Рис.
16. Троичная
m-наччи
система, где каждая пара двоек отделена как минимум одним нулем (m=3)
ИЗМЕРЕНИЕ ИЗБЫТОЧНОСТИ
В работе Butler and
Sasao [4] мы ответили на следующий вопрос:
Каковы границы избыточности в избыточных системах?
Этот вопрос
возникает всякий раз, когда мы накладываем ограничения на записи в той или иной
системе.
Скажем, мы хотим
узнать границы, до которых ограничение «без смежных единиц» делает набор
записей пригодным для представления чисел в системе Фибоначчи. Мы можем оценить
избыточность двумя способами:
1)
по
количеству записей, пригодных для представления чисел;
2)
по
доле тех или иных цифр среди всех записей.
Например, мы
предполагаем, что ограничение «без смежных единиц» понижает количество единиц в
сравнении с количеством нулей. Нас интересуют границы, до которых это
происходит. Мы получили распределение для неизбыточных представлений в
Фибоначчи, Трибоначчи, Квадраначчи и т.п. системах. В частности, на Рис.17
показано распределение количества 16-битных представлений по количеству единиц.
Эти представления задаются формулой:
N = a15F17 + ... + a2 F4 +
a1 F3 +
a0 F2, (1)
где Fi = Fi-1 + Fi-2 + ... +Fi-m , при i
> m+1
и Fi = 2i-2, при 1 < i ≤
m+1.
При m = 2, 3 и 4 формула (1) приводит к системе
Фибоначчи, Трибоначчи и Квадраначчи соответственно.
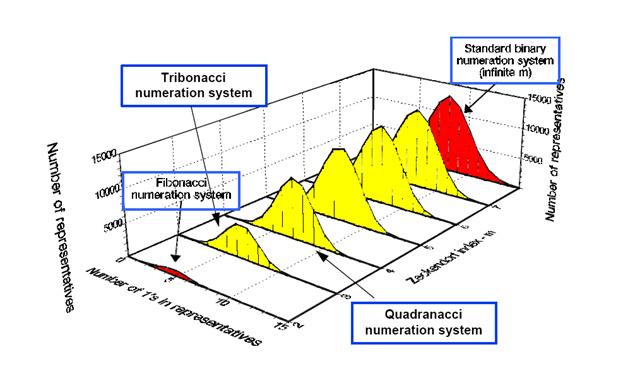
Рис.17.
Распределение неизбыточных представлений в 16-битных системах счисления
Любопытно,
что в системе Фибоначчи (с запретом на пары единиц) существует гораздо меньше
представлений, чем в системе Трибоначчи (с запретом на тройки единиц).
Рассмотрим далее, для сравнения, распределение единиц в стандартной двоичной
системе, что соответствует случаю m = ¥. Таблица 1 показывает долю единиц в разрешенных представлениях, для
относительно большого количества бит.
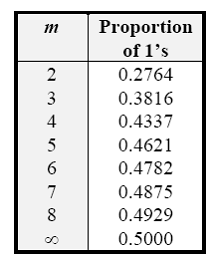
Табл.1. Доля
бит с единицей в различных системах
На
Рис.18 показано распределение единиц для обобщенных систем счисления Фибоначчи,
то есть для 16-битных систем, основание которых задано формулами:
Fi = Fi-1 + Fi-m при i > m+1,
Fi
= i-1 при 1 ≤ i ≤ m+1;
m ≥ 2
Как
и в предыдущем примере, при m
=
2 мы имеем обычную систему Фибоначчи. Интересно, что в этом случае число
представлений для m
=
2 значительно больше, чем для m
=
3.
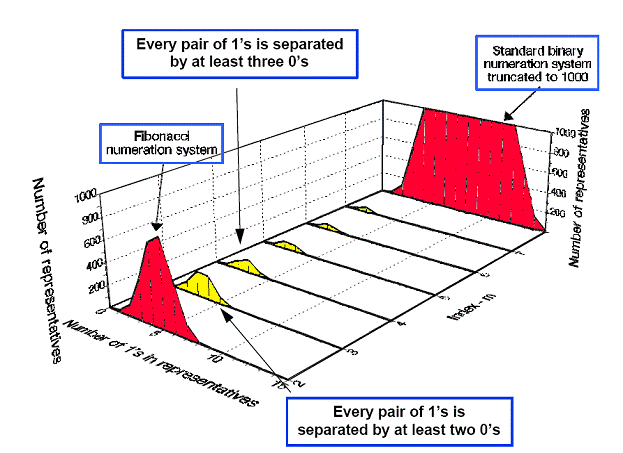
Рис.18.
Распределение неизбыточных представлений в 16-битных системах счисления
В таблице 2
приведено относительное количество цифр 0, 1, ... , m-1
в системах счисления m-наччи.
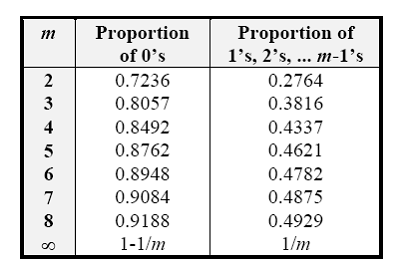
Табл.1. Доля
бит со значениями 0, 1, ... , m-1 в различных системах
ИЗБЫТОЧНОСТЬ
В АРИФМЕТИЧЕСКИХ ОПЕРАЦИЯХ
Kaneyama и
соавторы [11], а также Harata
и
соавторы [10] продемонстрировали преимущества избыточных систем в работе
недвоичных мультипликаторов. Эти преимущества демонстрирует следующий пример.
Пусть
целое N можно представить в виде:
N = an-12n-1 + ... + a222 + a121 + a020, где ai Î {0,1,2,3}.
Такая
система счисления избыточна; например, 101 = 021 = 5. Сложение в таких системах
не содержит длинных переносов через разряды. А именно, перенос происходит
только через 3 разряда. В результате, время, затраченное на вычисления,
невелико.
Рассмотрим
для примера сложение 10231 + 11111. Каждое из этих чисел в десятичной системе
равно 31, их сумма равна 62. На первом шаге сложим числа в столбик, не проводя
переносов. Обратим внимание, что в получившейся сумме Z присутствует цифра 4,
отсутствующая в данной системе. На следующем шаге переведем каждую цифру в ее
двоичный эквивалент. Так как максимальная цифра, которая может нам встретиться,
это 6 (3+3), то для представления любой цифры нам будет достаточно трех бит.
Строки C0, C1 и C2 содержат двоичные эквиваленты цифр из строки Z. Сложение строк C0, C1 и C2 дает нам
строку S; обратим внимание, что
максимально возможная цифра в этой строке равна 3. Таким образом, S является представлением суммы в рассматриваемой
системе счисления.

Рис.19.
Пример сложения в избыточной системе
При сложении
важно помнить, что перенос может случиться максимум через 3 позиции. На Рис.20 изображена
схема сумматора, выполняющего сложение по алгоритму из рис.19. На данной схеме
хорошо видно, как переносы влияют на сумму. Самая длинная последовательность
операций здесь – это Суммирование –
Преобразование в двоичный код – Суммирование.
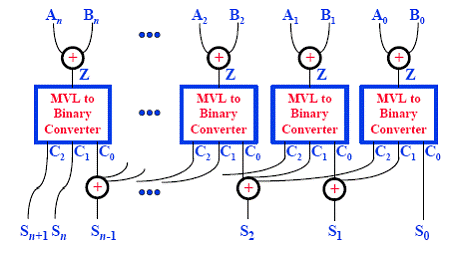
Рис.20.
Примерная схема сложения в избыточной системе
Заметим, что сложение выполняется
за фиксированное время; таким образом, время выполнения сложения не зависит от
количества цифр.
ЗАКЛЮЧЕНИЕ
Мы рассмотрели
здесь системы счисления, как двоичные, так и недвоичные, как избыточные, так и
неизбыточные. В то время, как неизбыточные системы способны представлять
большее количество чисел, избыточные имеют преимущества при передаче и хранении
информации, а также преимущества для быстрого выполнения арифметических
операций.
СПИСОК ЛИТЕРАТУРЫ:
1. J. L. Brown,
“Zeckendorf’s theorem and some applications,” The Fibonacci Quarterly Vol.
2.2 1964, pp. 163-168.
2. J. L. Brown, “A new characterization
of the Fibonacci numbers” The Fibonacci Quarterly, Vol. 3.1, 1965, pp.
1-8.
3. M. W. Bunder, “Zeckendorf
representation using negative Fibonacci numbers,” The Fibonacci Quarterly,
May 1992, pp. 111-115.
4. J. T. Butler and T.
Sasao, “On the proportion of digits in redundant numeration systems,” The
Fibonacci Quarterly, Vol. May 1997, pp. 172-180.
5. R. M. Capocelli, G.
Gerbone, P. Cull, and J. Hollaway, “Fibonacci facts and formulas,” and
“Sequences” in Int. Conf. on Combinatorics, Compression, Security, and
Transmission, Ed. R. M. Capocelli, New York: Springer-Verlag, 1990, pp.
133-137.
6. D. H. Davies, “The CD-ROM
medium,” J. Amer. Soc. for Inform. Sci. Vol. 39.1, 1988, pp. 34-42.
7. V. S. Dimitrov and B. D.
Donevsky, “Faster multiplication of medium large numbers via the Zeckendorf
representation,” The Fibonacci Quarterly, Vol. 33.1, 1995, pp. 74-75.
8. A. S. Fraenkel, “Systems
of numeration,” Amer. Math. Monthly, Vol. 92, 1985, pp. 105-114.
9. A. Glaser, History of binary
and other nondecimal numeration,
10.Y. Harata, Y. Nakamura,
H. Nagase, M. Takigawa, and N. Takagi, “A high-speed multiplier using redundant
binary adder tree,” IEEE J. of Solid-State Cir., Feb. 1987, pp. 28-34.
11.M. Kameyama,
12.W. H. Kautz, “Fibonacci
codes for synchronization control,” IEEE Trans. on
Infor. Th., Vol. IT-11, 1965, pp. 284-292.
13.S. T. Klein,
“Combinatorial representations of generalized Fibonacci numbers,” The
Fibonacci Quarterly, Vol. 29.2, 1991, pp. 124-131.
14.P. Morrison and P.
Morrison, “The physics of binary numbers,” Scientific American, Feb.
1996, pp. 130-131.
15.J. Newman, The World
of Mathematics,
16.E. Zeckendorf,
“Representation des nombres naturels par une somme de nombres de Fibonacci ou
de nombres de Lucas,” Bull. Soc. Royale Sci. Liege 41, 1972, pp.
179-182.