1. Введение
Попытки сконструировать дробную
версию пуассоновского процесса были предприняты Репиным и Саичевым (2000) , Jumarie (2001) и Ласкиным (2003).
Идея конструирования дробного
процесса с помощью обычного пуассоновского (по аналогии с хорошо известным
случаем броуновского движения) встречается в статьях Wang’а сотоварищи (2006)-(2007).
Предложенный ими процесс сгенерирован с помощью стохастического интеграла по
мере Пуассона.
Мы пойдем совсем другим путем и
сконструируем несколько видов дробного пуассоновского процесса.
Наши главные результаты относятся
к дробному пуассоновскому процессу
Nν
(t),
t >
0,
распределение которого pk = Pr{Nν
(t) = k}, k ≥
0, является решением уравнения:
где
p−1(t) = 0 и pk(0)
удовлетворяет условию:
Применим
в формуле (1.1) определение дробной производной Dzerbayshan-Caputo:
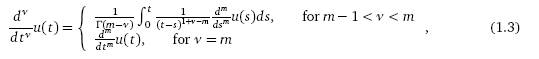
где m €
N (см. Podlubny (1999), стр.78)
Обратим внимание, что при ν = 1 (1.1) превращается в уравнение
однородного пуассоновского процесса, то есть мы обобщаем результаты для хорошо
известного распределения.
Решением для (1.1)-(1.2) является распределение процесса, который в
дальнейшем мы будем обозначать как Nν (t), t
> 0.
Представление дробной производной в виде (1.1) приводит к ряду выводов,
важнейшим из которых является независимость приращений Nν.
Мы будем использовать различные формы представления решения (1.1); вот
первая из них:
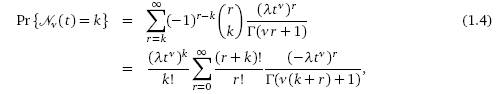
при
k ≥ 0, t > 0.
Распределение (1.4) совпадает с формулой (25) в статье Ласкина от
2003г., хотя оно было получено как решение уравнения (1.1) с дробной
производной в смысле Римана-Лиувилля, а не в смысле (1.3).
В работе Jumarie (2001) дробная производная также берется в смысле
Римана-Лиувилля, она входит в начальное условие и в результате опять получается
формула (1.4). В качестве базового материала по дробному исчислению рекомендуем
читать Самко сотоварищи (1993).
Другая форма записи данного распределения представлена в терминах
обобщенной функции Миттаг-Лефлера и определена следующим образом (см. Podlubny (1999), стр.17):
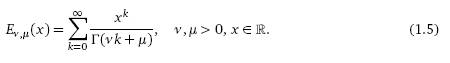
Для
небольших значений k получаются интересные выражения; например,
для k=0:
то есть распределение времени ожидания
первого пуассоновского события.
Мы можем доказать, что дробный пуассоновский процесс Nν (t), t>0, с распределением (1.4) связан с обычным
однородным пуассоновским процессом N (t), t>0 следующим
соотношением:
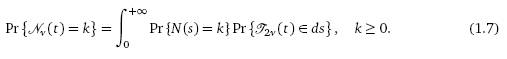
В (1.7) T2ν (t), t>0, - случайный процесс с распределением v2v = v2v (y, t),
удовлетворяющим следующей задаче Коши (для дробного уравнения диффузии):
с дополнительным условием: vt (y,0) = 0, for 1/2 < v < 1.
Соотношение (1.7) означает, что
дробный пуассоновский процесс Nν
имеет следующее представление:
и, следовательно, его можно рассматривать
как однородный пуассоновский процесс, остановленный в случайное время T2ν
(t).
На основе вышесказанного в Разделе 3 мы построим случайное блуждание на
плоскости, состоящее из движений с конечной скоростью c
и изменений направления через промежутки времени, определенные дробным
пуассоновским процессом Nν. Каждое изменение
направления происходит по равномерному закону на [0, 2π]. Это построение
является первой целью нашего исследования.
Для простейшего случая, когда процесс, управляющий изменениями
направления – стандартный пуассоновский, данная модель была исследована в
статье Kolesnik и Orsingher (2005). Условное
распределение случайного вектора (X(t), Y (t))
, t > 0 (представляющего позицию движущейся частицы в
момент t) задается как
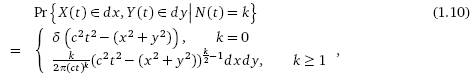
для t>0, (x, y) € Cct
= { x,
y:
x2+y2
≤
c2t2
}.
Мы получим аналог формулы (1.10) для дробного случая, т.е. для ν € (0, 1]. В частности, для случая
ν = 0.5, дробный процесс, управляющий изменениями направления, задается
формулой N1/2 (t)
= N(|B(t)|);
таким образом, в этом случае уравнение (1.8) сводится к уравнению теплопроводности.
Мы докажем, что условное распределение случайного вектора (X(|B(t)|), Y (|B(t)|)) , t
> 0
может быть записано так:
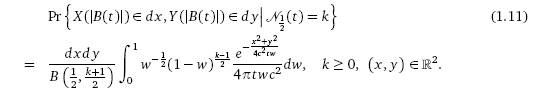
где
B(α, β) означает бета-функцию с
параметрами α,
β,
а B(t), t
> 0 –
стандартное броуновское движение, не зависящее от (X(t), Y (t)). Это означает, что движение на плоскости с броуновским временем
может быть рассмотрено как броуновское движение на плоскости с собственным
вероятностным распределением, обладающим свойствами бета-распределения,
зависящего от количества изменений направления.
Безусловный вариант распределения принимает интересные формы, особенно
– в некоторых частных случаях. Вообще, для ν € (0,1], мы имеем:
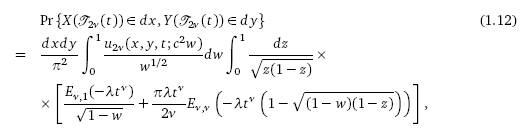
где
u2ν = u2ν (x, y, t; λ2) – фундаментальное решение
волнового уравнения для дробного случая (см. ниже (3.16)).
В случае ν = 1 предыдущее выражение приобретает следующую
интересную форму:
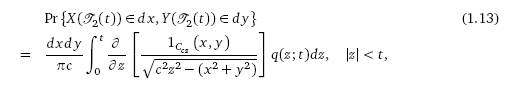
где
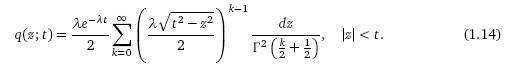
Распределение (1.14) –частное безусловное распределение случайного
блуждания по плоскости (X(t), Y (t)) , t > 0 (со скоростью, равной 1),
заданного формулой (1.3) в работе Orsingher, De Gregorio
(2007).
Функция-ядро в (1.13)
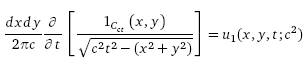
известна
из теории цилиндрических волн, занимающейся анализом следующей задачи:
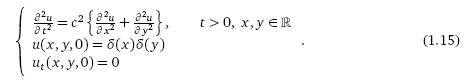
Раздел 4 посвящен исследованию
альтернативных форм дробного пуассоновского процесса. Первая из них,
обозначенная как 
,
определена как обобщение пуассоновского распределения на случай ν € (0,1] следующим
образом:
таким образом, его производящая функция выглядит
так:
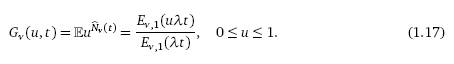
Как будет видно далее, для ν = 1 формулы (1.16) и (1.17) сводятся
к соответствующим результатам для стандартного пуассоновского случая. Данная
версия дробного пуассоновского процесса не обладает свойством независимости
приращений.
Мы докажем, что производящая функция (1.17) является решением дробного
уравнения:
Отталкиваясь от данной модели,
построим дробную версию сложного пуассоновского процесса, определенного (для
любого фиксированного t) как сумма случайного количества независимых и одинаково распределенных с.в., и
получим для этого процесса характеристическую функцию.
Кроме того, для двух первых версий
дробного пуассоновского процесса получим некоторые результаты, касающиеся
максимума, минимума и порядковых статистик последовательностей н.о.р.с.в., темп
поступления которых задается Nν
и .
В гидрологии и сейсмологии
последовательность катастрофических событий может быть представлена дробным
пуассоновским процессом, лишенным свойства отсутствия последействия, в отличие
от обычного пуассоновского. Оценка распределения максимума н.о.р.с.в., количество
которых определяется дробным пуассоновским процессом, имеет практическое
применение, т.к. позволяет определять вероятность экстремальных событий.
Третий процесс, 
,
t>0,
описанный в данной работе, есть процесс восстановления с временами между
событиями Uj , j ≥ 1, удовлетворяющими формуле (1.6):
Распределение можно выразить, для m ≥
0, так:
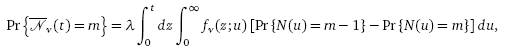
где
– плотность стационарных с.в.
Sν(μ, β, σ), μ = 0, β = 1, σ = (t cos πν/2)1/ν.
Раздел 2. Первая форма дробного пуассоновского процесса